Demo Vids: https://youtu.be/-i0PSxcoDH0, https://youtu.be/mzPUfs9sYQE, https://youtu.be/Z7D6obv12zk, https://youtu.be/LkDJ9XT-klU
Github Repository: https://github.com/mbird1258/Audio-Decomposition
Premise
My plan for this project was to create a program to turn music to sheet music. It was mainly incentivised by my own desire to turn music to sheet music and the lack (from what I could tell) of open source, simple algorithms to perform audio source separation.
Preparation
Instrument data
The instrument data all comes from the University of Iowa Electronic Music Studios instrument database. With these files, we find the Fourier transform of the entire wave and the envelope of the wave using the same method as documented below.
How it works
An instrument’s sound wave is mainly characterized by its fourier transform and envelope. Thus, we can use both of these to hopefully get a good idea of which instrument is playing what note.
Fourier Transform
The program’s first method of splitting music into constituent notes and instruments is by taking the fourier transform of the music file every 0.1 seconds (spectrogram), and adding together our stored fourier transform of each instrument to recreate the fourier transform of the 0.1 second window. The idea was to hopefully perfectly recreate the music at the set time as the fourier transform should represent the music played relatively well.
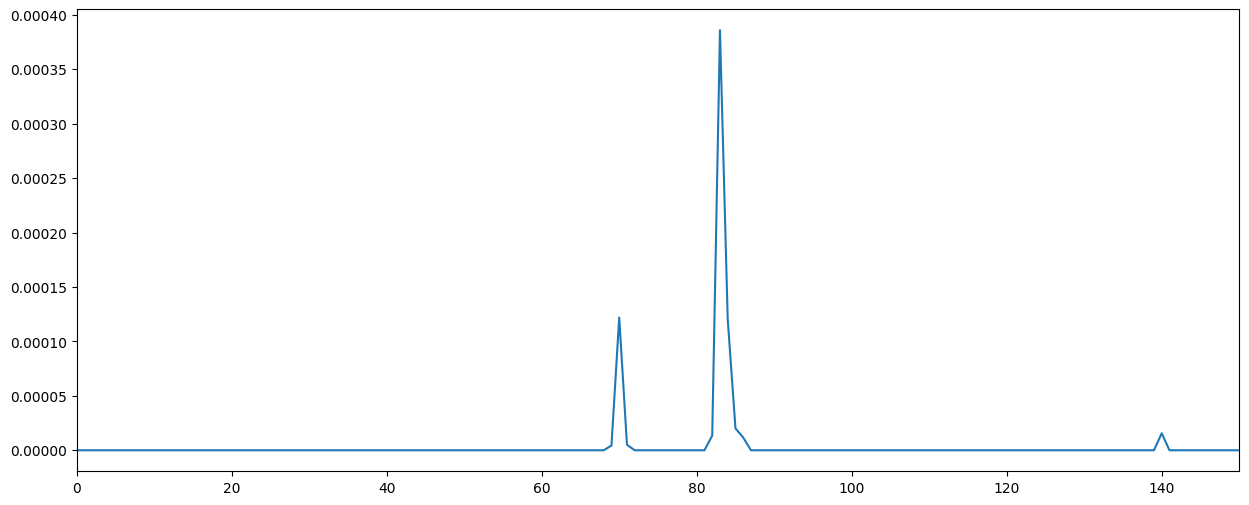
Original fourier transform
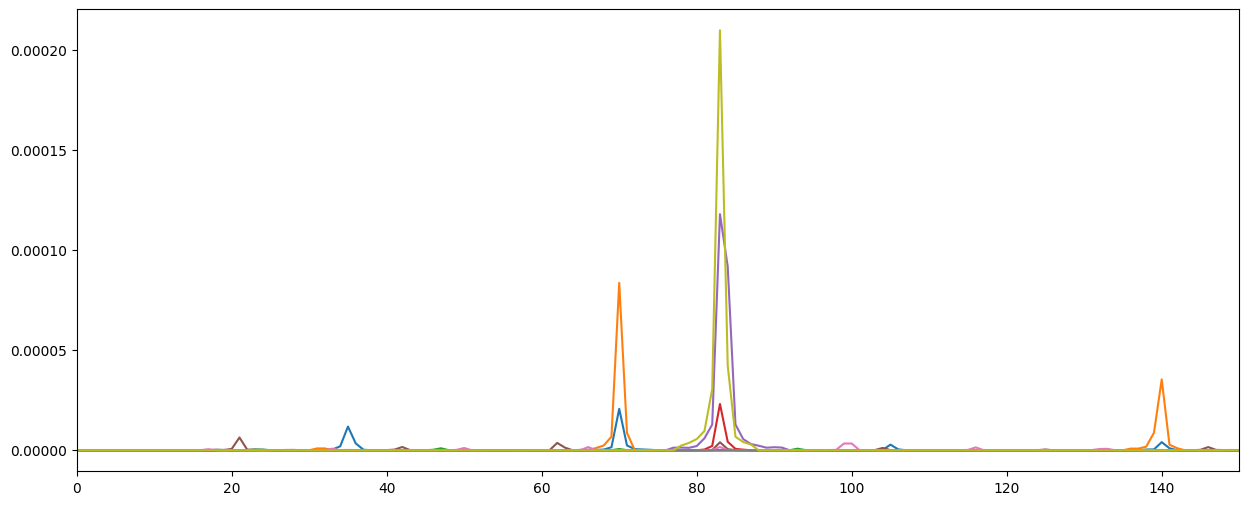
Constituent instruments
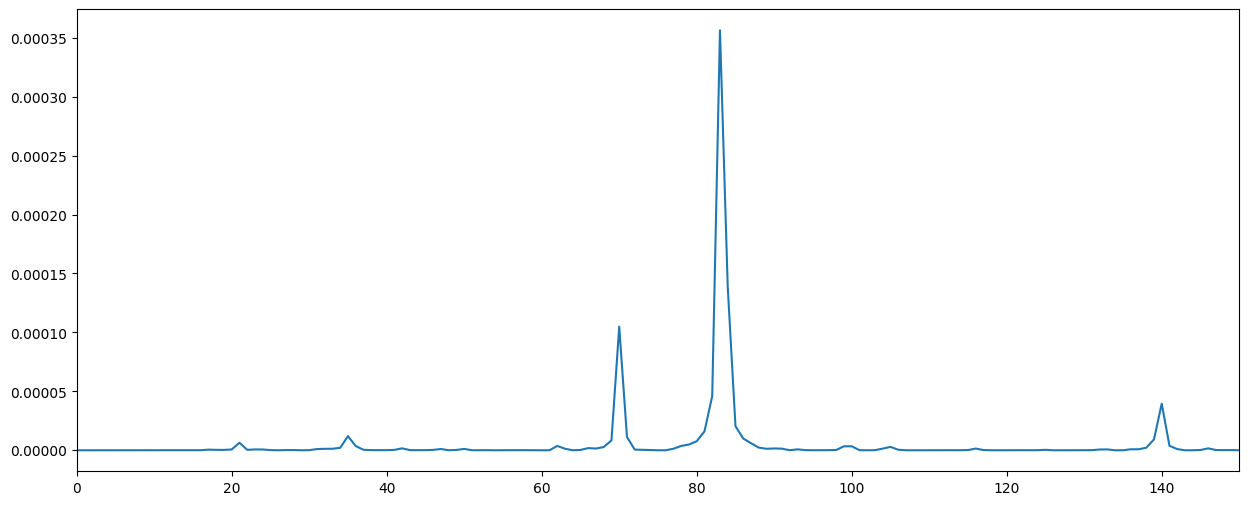
Recreated fourier transform
The magnitudes for each instrument are given by solving the following matrix. The matrix is derived from taking the partial derivative of the MSE cost function by frequency(ex. FT value at 5 hz) with respect to each instrument. Each row in the matrix is a different partial derivative. (First is w.r.t cello, second is w.r.t piano, etc.)

Envelope
The first step to matching the envelope of the instrument to the sound wave is to obtain the envelope itself. The envelope is the upper bound of a wave, and although there are functions to do this, they seemingly struggle with noise and certain types of sound waves. Thus, since we have to handle many different instruments at different frequencies, we need a more robust solution.
To get the envelope, the function splits the sound wave into chunks, before taking the max value at each chunk. To further refine the results, the function finds the points where the envelope is below the original sound wave and adds a new point defining the envelope.
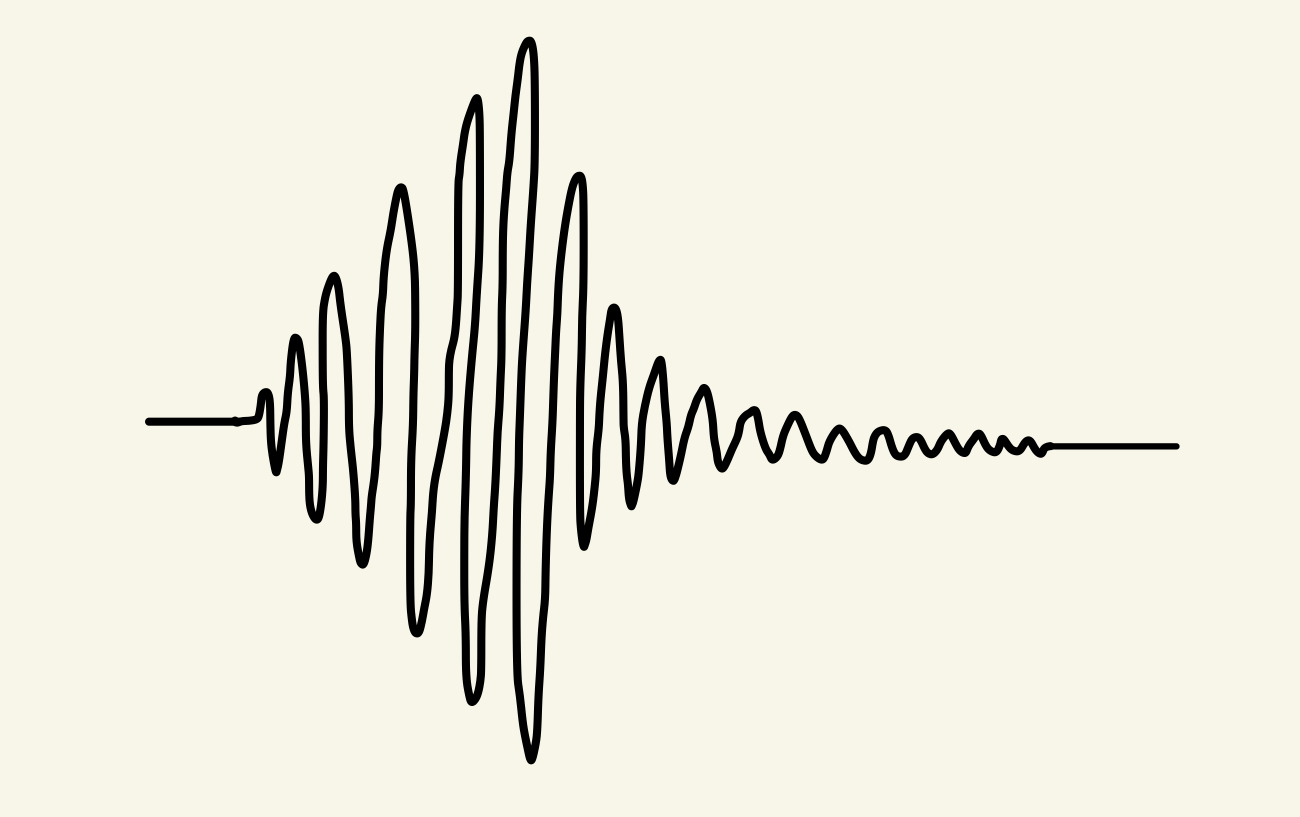
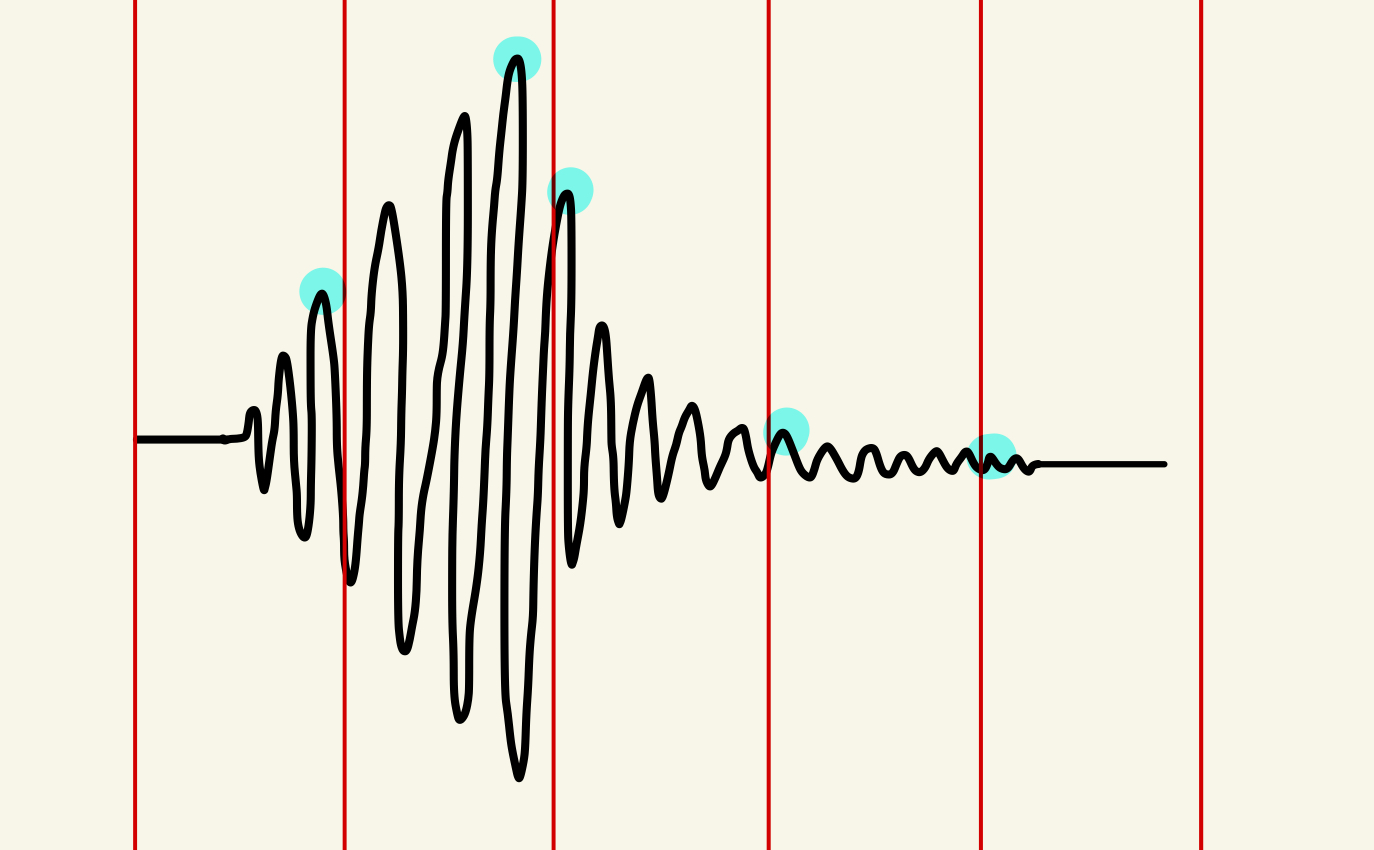
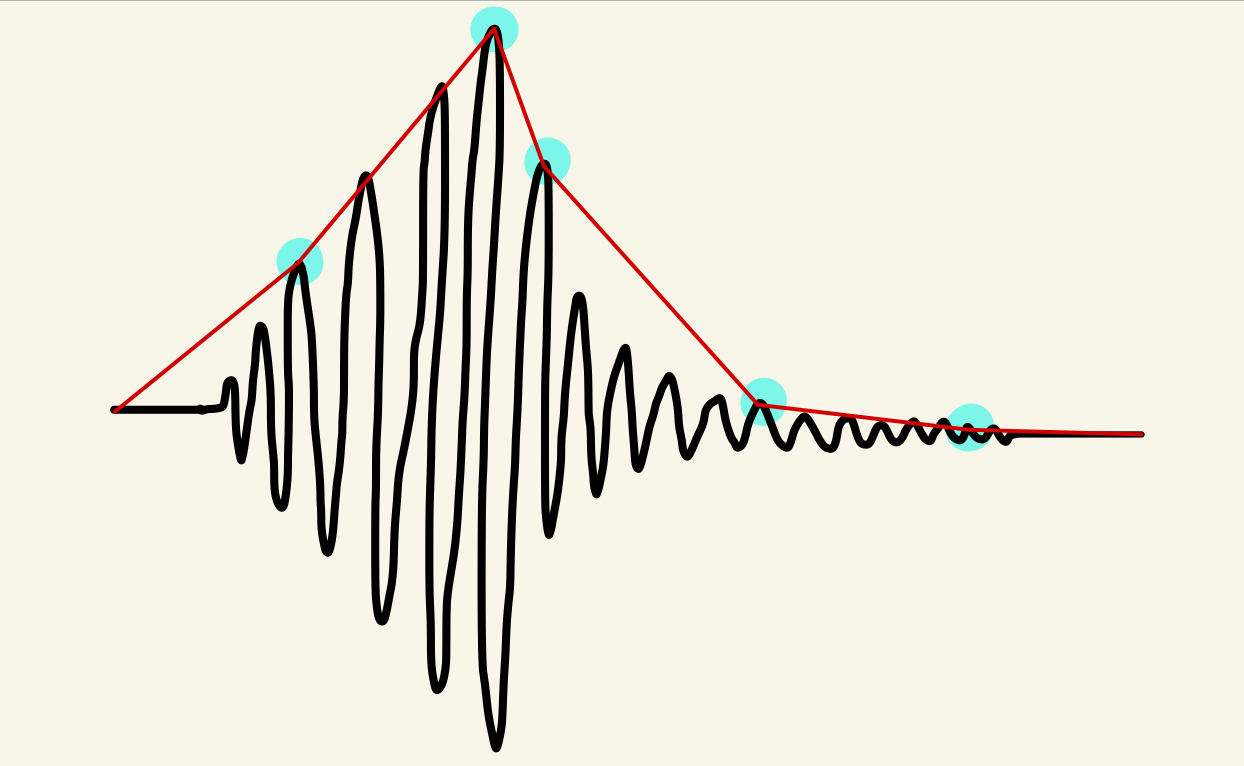
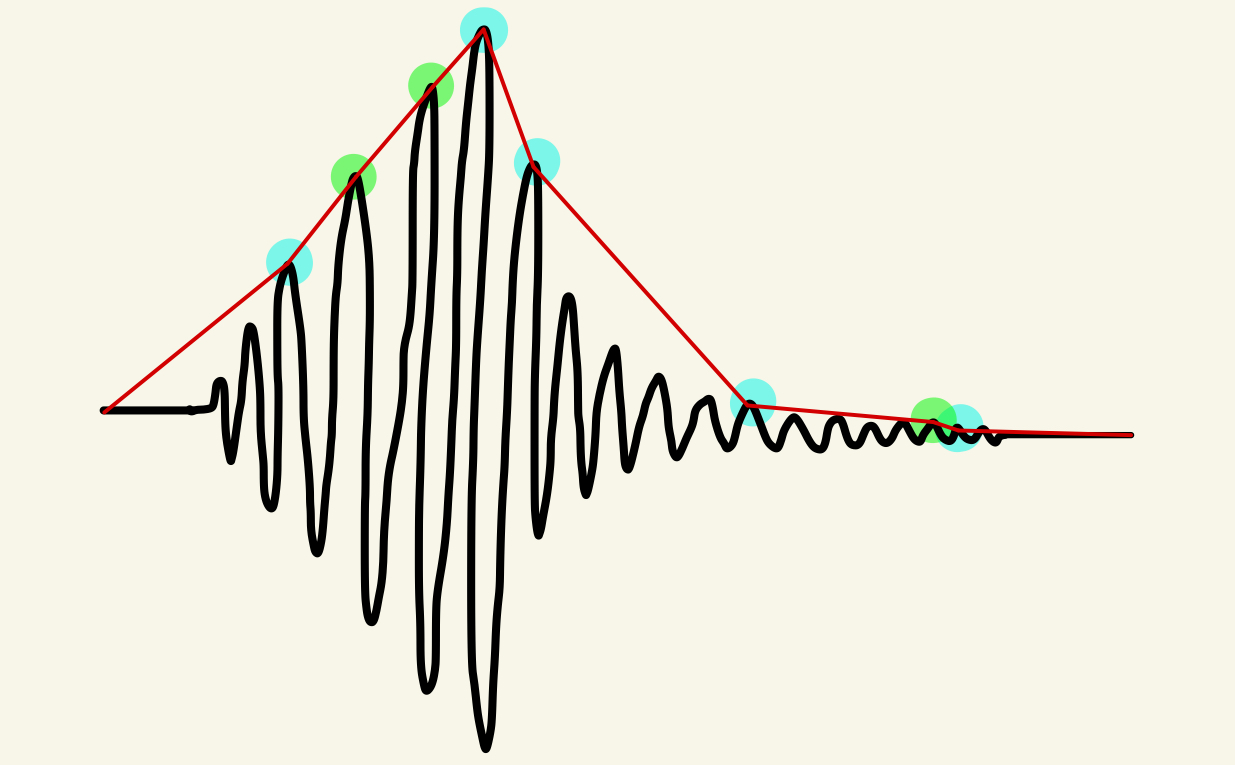
The next step is to split the envelope of the wave into its attack, sustain, and release. The attack is the initial noise of the note, the sustain is while the note is held, and the release is when the note stops. For the instrument samples, we can take the first nonzero value of the wave to get the start of the attack. To get the point between the attack and sustain, we get the first point when the function is concave down or decreasing. To get the point between the sustain and release, we get the first point from the end where the function is increasing or concave down. To get the end of the release, we find the first point from the end where the function is nonzero.
To further classify the wave, we need to take into account the main forms the wave can take. Some instruments, such as the piano, have static decay, in which they mostly follow an exponential decay shape. On the other hand, some instruments, like the violin, can increase or decrease in volume as the note is sustained. In addition to this, some audio samples in the instrument files are held until their sound expires, while others are released early. To differentiate whether the decay is static or dynamic, if the decay factor is >1, or if it deviates from the decay curve by too much, it’s dynamic. To differentiate if the envelope has a release or not(AS or ASR), we look at the average rate of change across the sustain and the release, and if the rate of change of the release is lower then there is no release.
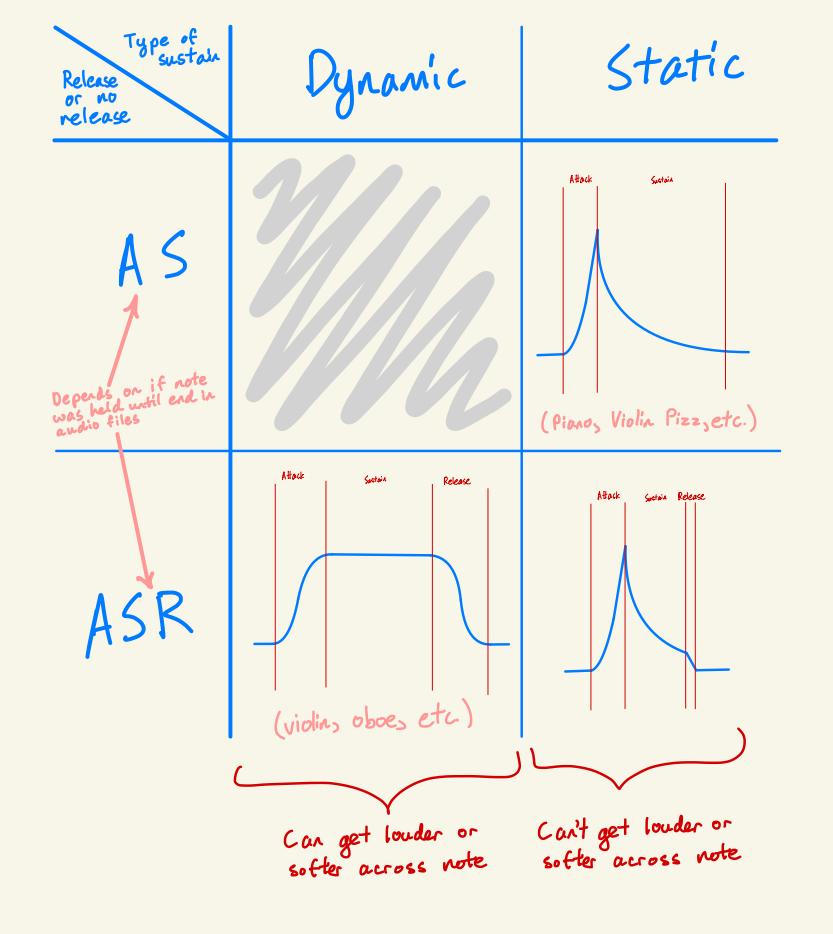
Different types of wave
To deal with the music file, we first take the bandpass filter of the signal for each note frequency. With the filtered wave, we iterate through each instrument. For each instrument, we take the cross correlation of the instrument’s attack(normalized) and release(normalized) to find the start and end of each note, and then take the MSE of the instrument wave and the filtered audio to get our cost for the instrument at that time. After this, we multiply the magnitude we found in the fourier transform step and 1/(cost we found in this step) to get our final magnitudes.
Display
To display the file, we use matplotlib’s scatter plot with - shaped points to display the sheet music. Originally, I wanted to recreate the audio from the magnitudes, but it led to many issues, took a while, and made troubleshooting much harder. I also tried using matplotlib’s imshow plot, but it’s extremely inefficient in this case as most values are 0, and matplotlib needs to redraw every point regardless of if it’s on screen or not every time we pan or zoom the screen.
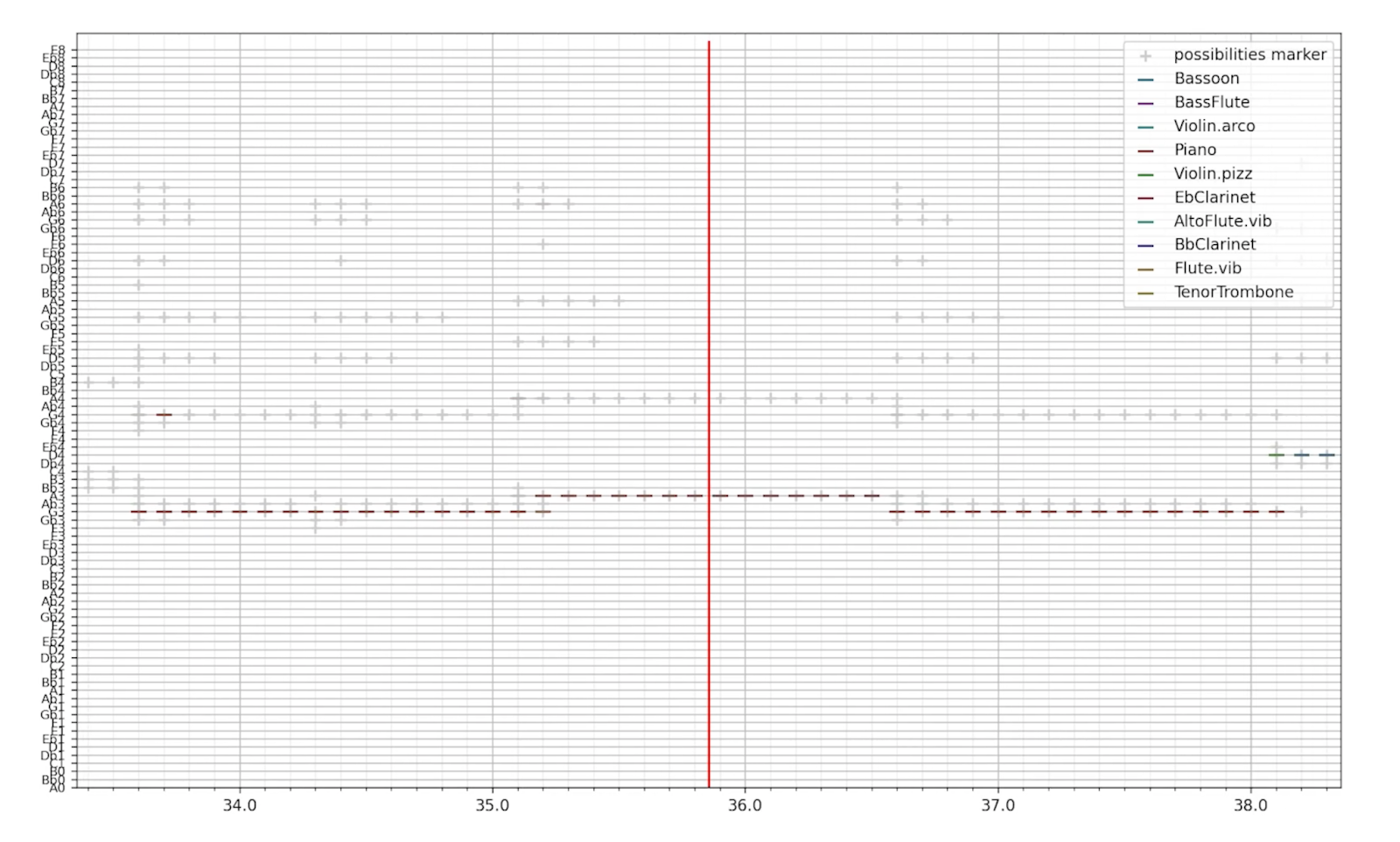
Results
Overall, I think it works quite well. You can use it to make recreating sheet music better(as I did here from this video), especially if you struggle with finding the right pitch or chords, and it doesn’t take too much time to run either.